ฟังก์ชันขั้นบันได

ฟังก์ชันขั้นบันได คือฟังก์ชันบนจำนวนจริงซึ่งเกิดจากการรวมกันระหว่างฟังก์ชันคงตัวจากโดเมนที่แบ่งออกเป็นช่วงหลายช่วง กราฟของฟังก์ชันจะมีลักษณะเป็นส่วนของเส้นตรงหรือรังสีในแนวราบเป็นท่อน ๆ ตามช่วง ในระดับความสูงต่างกัน อ่านเพิ่มเติม

ฟังก์ชั่นค่าสัมบูรณ์

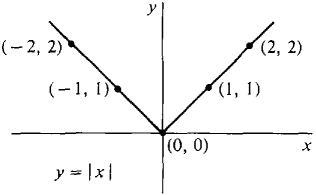ฟังก์ชันค่าสมบูรณ์ถูกกำหนดโดยกฎซึ่งแบ่งออกเป็นสองกรณีค่าฟังก์ชันสมบูรณ์ | | จะกำหนดโดย อ่านเพิ่มเติม

ฟังก์ชันเอกซ์โพเนนเชียล

ฟังก์ชันนั้นมีอยู่หลายรูปแบบ แต่ละแบบก็มีการตั้งชื่อไม่เหมือนกัน ฟังก์ชันเอกซ์โพเนนเชียลก็เป็นอีกรูปแบบหนึ่งของฟังก์ชันซึ่งเราจะไปดูว่าฟังก์ชันเอกซ์โพนเนนเชียลนั้นมีรูปแบบอย่างไร ก็ต้องไปดูนิยามของมันครับ ว่านิยามของฟังก์ชันเอกซ์โพเนนเชียล อ่านเพิ่มเติม

ฟังก์ชั่นกำลังสอง

ฟังก์ชันกำลังสอง  คือ  ฟังก์ชันที่อยู่ในรูป  เมื่อ  a,b,c  เป็นจำนวนจริงใดๆ  และ ลักษณะของกราฟของฟังก์ชันนี้ขึ้นอยู่กับค่าของ  a , b  และ  c  และเมื่อค่าของ  a  เป็นบวกหรือลบ  จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ  อ่านเพิ่มเติม

ฟังก์ชั่นเชิงเส้น

ฟังก์ชั่นที่อยู่ในรูป f(x) = ax+b  เมื่อ a และ b เป็นจำนวนจริงเช่น f(x) = 2x+1  

f(x) = -3x     f(x) = x-5 เป็นต้น   กราฟของฟังก์ชั่นเหล่านี้เป็นเส้นตรงที่ไม่ขนานกับแกน ฟังก์ชั่นเชิงเส้น f(x) = ax+b เมื่อ a=0 จะได้ฟังก์ชั่นอยู่ในรูป f(x) = b ฟังก์ชั่นนี้มีชื่อเรียกเฉพาะ อ่านเพิ่มเติม

ฟังก์ชัน

ในทางคณิตศาสตร์ "ฟังก์ชัน" บัญญัติขึ้นโดย ไลบ์นิซ ใน พ.ศ. 2237 เพื่ออธิบายปริมาณที่เกี่ยวข้องกับเส้นโค้ง เช่น ความชันของเส้นโค้ง หรือจุดบนเส้นโค้ง ฟังก์ชันที่ไลบ์นิซพิจารณานั้นในปัจจุบันเรียกว่า ฟังก์ชันที่หาอนุพันธ์ได้ และเป็นชนิดของฟังก์ชันที่มักจะแก้ด้วยผู้ที่ไม่ใช่นักคณิตศาสตร์ สำหรับฟังก์ชันชนิดนี้ เราสามารถพูดถึงลิมิตและอนุพันธ์ ซึ่งเป็นการทฤษฎีเซต พวกเขาได้พยายามนิยามวัตถุทางคณิตศาสตร์ทั้งหมดด้วย เซต ดีริคเลท และ โลบาเชฟสกี ได้ให้นิยามสมัยใหม่ของฟังก์ชันออกมาเกือบพร้อมๆกัน  อ่านเพิ่มเติม

โดเมนและเรนจ์

ถ้าพิจารณาเฉพาะเซตของสมาชิกตัวหน้า และเซตของสมาชิกตัวหลังในคู่อันดับของความสัมพันธ์ใด ๆ จะได้โดเมน (domain) และเรนจ์ (range) ของความสัมพันธ์นั้นตามลำดับ
เช่น r1 = {(1,2),(2,3),(3,4),(4,5)} อ่านเพิ่มเติม